Head
Derangement model of ligand-receptor
binding
Large N limit of the knapsack problem
Permanents through probability
distributions
Self-assembly of a dimer system
Missing curriculum in physics problem solving
education
Permutation glass
Statistical physics of the symmetric
group
Multi SUSY breaking
Research
Current and past research projects
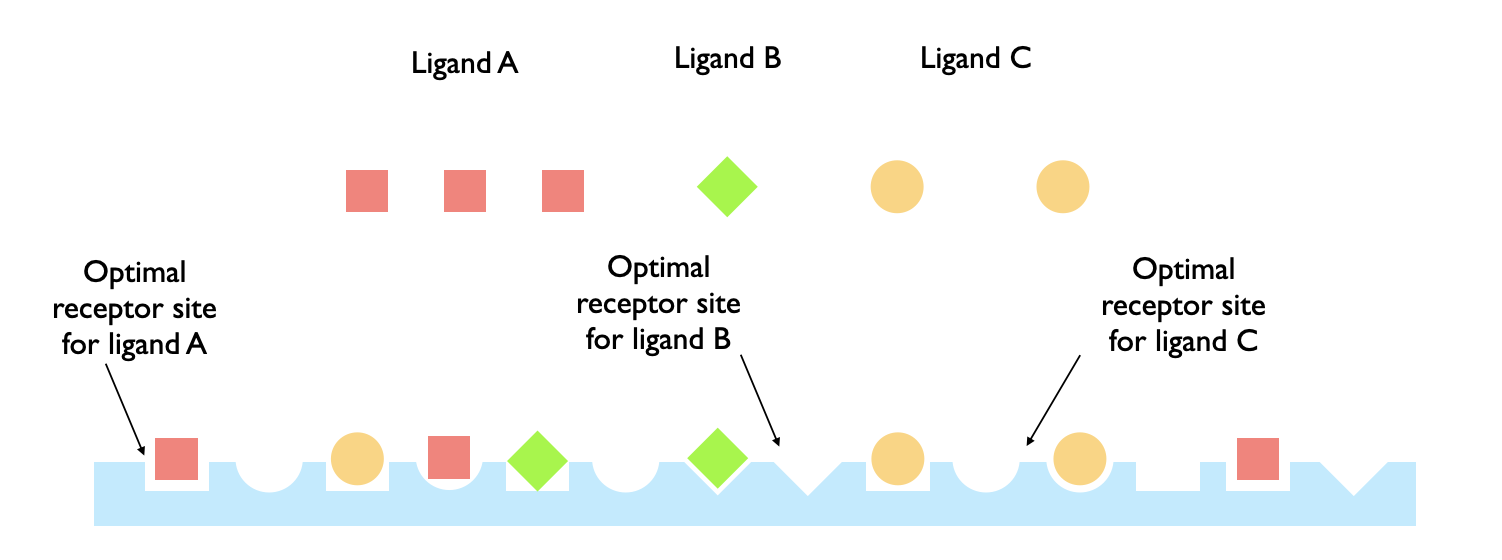
Ligands are proteins that exist outside a cell and attach to other proteins on the surface of a cell to initiate cell signaling pathways. Often these ligands can have optimal binding with a single type of receptor even while being able to bind to other receptors. If there are many such ligands all of which is in an environment where their optimal receptors exist with many sub-optimal ones, how can optimal ligand-receptor binding occur?
This work builds a model to explore this question. The model relies on an extension to Gillis and Even's formula for generalized derangements and ultimately computes observables that are checked by simulating a grid-based version of the system.
Supplementary Code: (Github Repository for "Combinatorial model of ligand-receptor binding")
Large N limit of the knapsack problem (Summer 2021)
(One Page Summary)/[arxiv:2107.14080]completed in Jellyfish Research

As the number of degrees of freedom of combinatorial optimization algorithms increases so too does their computation time (i.e., time-complexity). But approximation statistical physics calculations become more accurate as their degrees of freedom increase with little sacrifice in computation time.
You are given a set of objects each with a particular value and weight. Then you are given a knapsack which can only hold a maximum weight. You are then told to find the subset of objects with a maximum total value subject to the weight limit of the knapsack.
This task is called the knapsack problem. There are many exact and approximate algorithms to solving this problem, each of varying computational complexity. This is generally true for problems in the area of combinatorial optimization where one seeks to find various combinations of elements that optimize a certain objective.
In this work we represent the knapsack problem as a system in statistical physics and use the saddle point approximation to derive an algorithm for it in in the limit of a large number of items. The algorithm only yields approximate solutions and it's properties suggest that it is similar to a greedy approach to optimization.
Supplementary Code: (Github Repository for "Large N limit of the knapsack problem")
Permanents through probability distributions (Summer 2021)
(One Page Summary)/[arxiv:2106.11861]completed in Jellyfish Research

Relationship between the main theorem ("Theorem 1") proved in the work and other theorems and results associated with permananets.
The permanent is a strange object in mathematics. It looks like the determinant but it is notoriously more difficult to compute since it has none of the symmetry properties of its more famous cousin. In the most naive approach to calculating the permanent of an N by N matrix, one needs to enumerate and sum all the N! terms that enter into calculation. This becomes computationally intractable for large matrices, so much of the research work on permanents involves finding ways to reduce this computation time. Glynn's theorem is a famous result in this latter space since it reduces the N! terms to 2^N terms.
This paper shows how two results relating to permanent calculations stem from a more general theorem in which permanents can be calculated as the expectation values of probability distributions of a specific type. The work then fills in the gap in the network of these results to show how another permanent result is implied.
Self-assembly of a dimer system (Spring 2019)
(One Page Summary)/[arxiv:1909.00455]completed in Shakhnovich Biophysics Group
Say that many couples enter a dance hall. Immediately afterwards, the people in each of the couples separate and mingle so that at a later time some people are alone and other people are paired up in possibly new couples. For this repairing, each person has the highest affinity to be with the person he or she originally came with and a lower affinity to be with anyone else, however, since each person has only one high-affinity partner, there is a greater likelihood for a person to find a lower-affinity partner. With these constraints, how can we determine the average number of people who are alone and the average number of people who are with their original partner at the later time?

The combinatorial problem at the heart of the physics of dimer system self-assembly.
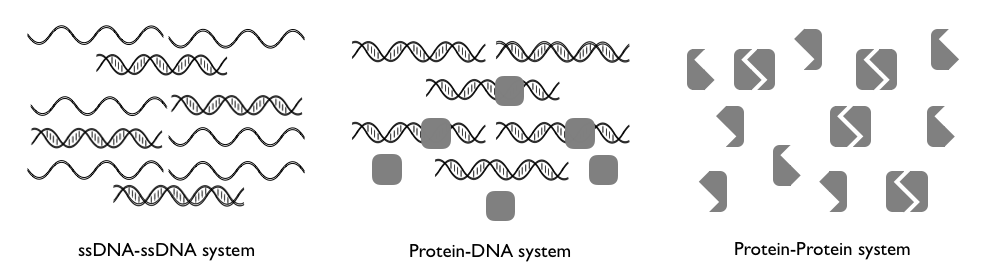
This combinatorial problem maps onto the problem of biomolecules (e.g., proteins, DNA) with promiscuous interactions. For the most part, biomolecule-biomolecule interactions within a cell are very specific with each biomolecule having a high affinity to its correct binding site or correct partner biomolecule. However, each biomolecule also often has a small affinity to other biomolecules, biomolecules that are usually so numerous that they can effectively compete with the high-affinity interaction. This work builds analytical models of these biomolecular interactions in order to understand the conditions under which the correct (i.e., high affinity) interactions dominate in protein-protein and protein-DNA systems. Ultimately, we find that self-assembly in these systems is most limited by the product between monomer diversity and volume.
Supplementary Code: (Github Repository for "Self-assembly of a dimer system")
Missing curriculum in physics problem-solving education (Spring 2018)
Sci and Educ (2018)completed with help from Harvard's Graduate Writing Center
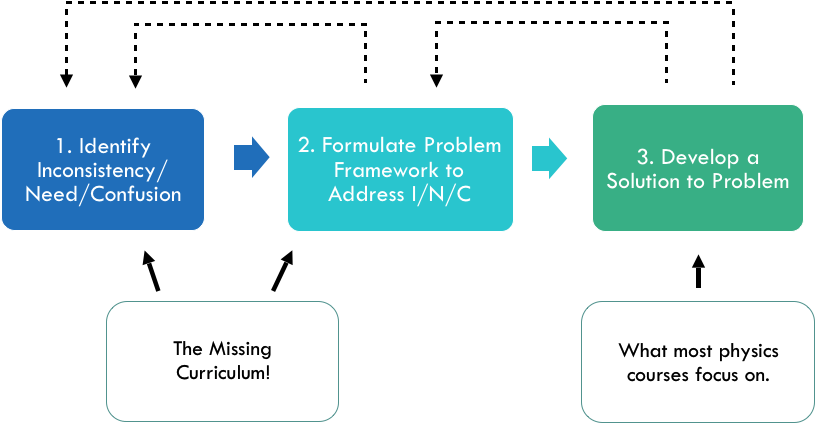
A problem solving process which takes into account the need to identify a need or inconstincency and develop a problem framework before the standard heuristics of problem-solving are applied. Physics courses usually give students practice in the final step. The first two steps constitute the missing curriculum.
Going through a physics course (not to mention an entire physics undergraduate curriculum) requires solving many problems. The main goal in tasking the student with so many problems is to have him or her develop a deeper knowledge of the principles underlying physical phenomena. A secondary goal—and a common reason for why physics majors are even for those who don't intend to become physicists—is that solving physics problems cultivates problem solving ability in general. In this paper I argue that this second goal is unlikely due to the nature of the problems most commonly assigned.
Permutation glass (Summer-Fall 2017)
(One Page Summary)/[arxiv:1801.03231]completed in Shakhnovich Biophysics Group

Four microstates of an example permutation system. The number of diagonal lines (labeled j), represents the number of incorrectly ordered components of the permutation and defines the permutation's energy.
Although material scientists make extensive use of various kinds of glasses, physicists do not understand glasses as well as they understand other systems like ideal gases or crystalline solids. Consequently, in order to build some understanding of glassy systems, physicists construct models which bear some of the basic properties of glasses (like disorder) without the more precise structural properties (like varying randomized bonding in multiple dimensions) which make glasses difficult to analyze in general. In this category are spin glasses which consist of taking the interactions between spins on a lattice to be random.
This paper considers "permutation glasses" which are more abstract models of disorder consisting of a state space of permutations where the energies of each permutation are random much in the same way spin glass interaction energies are random. The main result of the model shows that this energy disorder can contribute to thermal disorder, thus making the system less tolerant of high temperatures. The results of this paper expand our understanding of how disorder affects to systems with many degrees of freedom and also how such disorder can be manifest in abstract physical systems.
Supplementary Code: (Github Repository for "Permutation glass")
Statistical physics of the symmetric group (Spring 2016-Spring 2017)
(One Page Summary)/ PhysRevE.95.042126completed in Shakhnovich Biophysics Group

Four microstates of an example permutation system. The number of diagonal lines (labeled j), represents the number of incorrectly ordered components of the permutation and defines the permutation's energy.
A well known problem in molecular biology concerns how sequences of amino acids are related to the 3D structure of the protein they form. The problem has two related manifestations: the protein folding problem which attempts to determine, given a sequence of amino acids, what particular three-dimensional structure results, and the protein design problem (also termed, the "inverse-folding problem") which seeks, given a particular three-dimensional structure, what amino acid sequences fold into that structure
Some theoretical attempts to probe the protein design problem rely on a spin-lattice model of amino acids, but given the features of the problem it seems more appropriate to consider a state space of permutations rather than spins. With this motivation, the goal of the "Statistical Physics of the Symmetric Group" work was to explore the basic statistical physics of systems whose state spaces consisted of various permutations of an ordered list.
Multiple SUSY breaking as a model of dark matter (Fall 2012 - Summer 2013)
Undergraduate Thesiscompleted under Jesse Thaler

The image on the left shows the decay process studied in my thesis. In this process, a pseudo-goldstino decays into a gravitino (the superpartner of the graviton) and a photon. The image on the right represents the supersymmetry breaking scenario which leads to the particle spectrum (specifically, the gravitino and pseudo-goldstino) needed for the decay. The larger goal of the entire project was to develop a model of dark matter which could be compared with then recent Fermi Telescope results (https://arxiv.org/abs/1204.2797)